♦Con cinco conectivas lógicas básicas se construyen proposiciones compuestas que pueden ser tautologías, contradicciones o contingencias.
Si la tabla de verdad de la proposición es siempre verdadera, independientemente de la verdad o falsedad de las proposiciones simples, entonces la expresión estautológica.
Si la tabla de verdad es siempre falsa, será unacontradicción.
Si es verdadera y falsa, la proposición es unacontingencia.
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
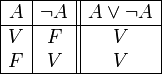
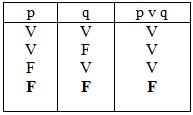
•TAUTOLOGÍA: Una proposición compuesta es una tautología si es verdadera para todas las asignaciones de valores de verdad para sus proposiciones componentes. Dicho de otra forma, su valor V no depende de los valores de verdad de las proposiciones que la forman, sino de la forma en que están establecidas las relaciones sintácticas de unas con otras. Sea el caso: 
•CONTRADICCIÓN: Se entiende por proposición contradictoria, o contradicción, aquella proposición que en todos los casos posibles de su tabla de verdad su valor siempre es F. Dicho de otra forma, su valor F no depende de los valores de verdad de las proposiciones que la forman, sino de la forma en que están establecidas las relaciones sintácticas de unas con otras. Sea el caso: 
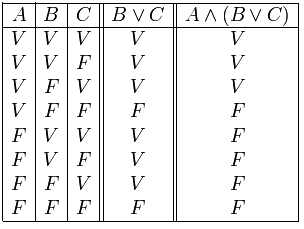
•CONTINGENCIA:Se entiende por verdad contingente, o verdad de hecho, aquella proposición que puede ser verdadera o falsa,(combinación entre tautología y contradicción) según los valores de las proposiciones que la integran. Sea el caso: 
Tablas de Verdad.
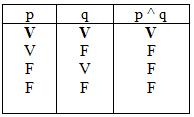
•CONJUNCIÓN: La regla para establecer los criterios de verdad de la conectiva lógica conjunción es la siguiente:
Una conjunción de enunciados en los cuales todos son verdaderos, es verdadera.
Una conjunción de enunciados en donde no todos son verdaderos es falsa.
Lo que equivale a decir que basta que uno de sus componentes sea falsa para que toda la proposición sea falsa y sólo será verdadera en el caso de que ambos componentes lo sean.
“El auto enciende cuando tiene gasolina en el tanque y tiene corriente la bateria”
(v) p: Tiene gasolina el tanque. ✓
(v) q: Tiene corriente la bateria. ✓
(v) r: El auto enciende. ✓
⇩ ⇩ ⇩
(v) p: Tiene gasolina el tanque. ✓
(f ) q: No tiene corriente la bateria. ✘
(f ) r: El auto no enciende. ✘
⇩ ⇩ ⇩
(f ) p: No tiene gasolina el tanque. ✘
(f ) q: No tiene corriente la bateria. ✘
(f ) r: El auto no enciende. ✘
•DISYUNCIÓN: La disyunción es verdadera, si al menos una de las proposiciones componentes es verdadera, resultando falso únicamente cuando las dos proposiciones son falsas.
Una disyunción inclusiva es verdadera cuando por lo menos una de sus alternativas es verdadera; solamente será falsa si las dos lo son.
“Una persona puede entrar al cine si compra un boleto o si obtiene un pase”
(v) p: Compra un boleto. ✓
(v) q: Obtiene un pase. ✓
(v) r: Una persona entra al cine. ✓
⇩ ⇩ ⇩
(v) p: Compra un boleto. ✓
(f ) q: No obtiene un pase. ✘
(v) r: Una persona entra al cine. ✓
⇩ ⇩ ⇩
(f ) p: No compra un boleto. ✘
(f ) q: No obtiene un pase. ✘
(f ) r: Una persona no entra al cine. ✘
•CONDICIONAL: expresada por la frase “si,… entonces”, se simboliza mediante el signo “→” colocado entre las dos proposiciones.. La primera proposición lleva el nombre de antecedente y la segunda proposición la de consecuente.
La condicional será falsa sólo cuando el antecedente es verdadero y el consecuente es falso, en los demás caso será verdadera.
 “Si me saco la loteria entonces te regalaré un carro”
“Si me saco la loteria entonces te regalaré un carro”
(v) p:Si me saco la loteria. ✓
(v) q: Te regalaré un carro. ✓
(v) p→q: Si me saco la lotería entonces te regalaré un carro. ✓
⇩ ⇩ ⇩
(v) p:Si me saco la loteria. ✓
(f ) q: No te regalaré un carro. ✘
(f ) p→q: Si me saco la lotería entonces no te regalaré uncarro.✘
⇩ ⇩ ⇩
(f ) p: Si no me saco la loteria. ✘
(f ) q: No te regalaré un carro. ✘
(f ) p→q: Si no me saco la lotería entonces no te regalaré un carro. ✓
•BICONDICIONAL: expresada por la frase “si y solo sí…”, denotada por el signo“↔”, significa una relación bidireccional en donde ambas proposiciones se necesitan entre sí.
La conectiva bicondicional será verdadera solamente si y solo si las dos sentencias que la componen son a la vez verdaderas o si son ambas falsas.
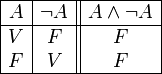

Gracias por el aporte
ResponderEliminarMuy interesante este tema ....Tablas de verdad*.
ResponderEliminar